<Generative model>
Generative model(생성 모델) 기존의 데이터셋 X의 분포를 근사하는
새로운 data를 생성하는 것으로 기존의 데이터셋 x이 나타날 수 있는 확률 분포 p(x)를
구하는 것이라고 생각할 수 있습니다. 이는 기존의 discriminative model과는
차이점이 있는데, discriminative model이란 데이터 x가 주어졌을때, 그에 해당하는 레이블
Y가 나타날 수 있는 조건부 확률 P(x|y)를 구하는 것 입니다. 그렇기 때문에 discriminative model은
레이블 y정보가 있어야 하기 때문에 supervised learning의 범주에 속합니다.
이와 반대로 generative model은 레이블 y에 대한 정보없이 데이터 x를 주고 P(x|x) = P(x)로
근사하는 확률 분포를 찾는 semi-supervised learning이라고 할 수 있습니다.
이러한 generative model을 활용한 대표적인 딥러닝 기술로 현재 무궁무진하게 발전하고 있는
GAN(generative adversial network)가 있습니다. GAN의 기본적인 학습방향을 쉽게 얘기한다면 서로
반대되는 목적을 가진 모델 2개가 서로 상충하는 목표를 향해 학습하면서 서로를 이기기 위해 더욱 발전하는 구조로 만들어져 있습니다.
현재까지 정말 다양한 GAN의 구조가 논문으로 나왔고, 이에 관련된 정보는
추후에 깊게 공부하여 자세하게 업로드를 하도록 하겠습니다.
<Metric for generative model>
해당 리뷰에서는 이런 generative model을 활용하여 생성된 data가 잘 생성이 되었는지 평가할 수 있는 metric에
대해 연구한 논문을 소개해보겠습니다.
예를 들어 image를 생성한다고 하면, 얼마나 image가 generative model을 학습시킨 dataset과 비슷한지,
얼마나 사람의 눈으로 보기에 natural한 image인지, 실제 이미지에 비해 얼마나 다양한 이미지를 생성하는지 등등 생성된 이미지의 품질을 평가할 수 있는 척도가 존재합니다. 이렇게 다양한 척도가 존재하고 그것이 좋다 안좋다를
평가할 수 있는 기준 또한 인간마다 다르기 평가할 수 있기 때문에 정확한 기준을 정립하는 것이 어렵습니다.
그렇기에 해당 논문에서는 이러한 모호함을 없애기 위해 노력합니다. 논문 제목에서도 알 수 있듯이 reliable metric입니다. 사람의 주관적인 기준에 따른 평가가 아닌 객관적인 평가를 할 수 있는 metric을 제안하고 있습니다.
이를 위해 논문에서는 생성된 이미지를 평가하는 기준을 2개로 정의합니다. 바로 fidelity와 diversity입니다.
Fidelity는 생성된 이미지의 품질입니다. 얼마나 natural한 이미지를 생성했는지, 원본과 비교했을 경우
큰 차이가 없는지 등을 평가하는 것이 여기에 포함됩니다. 그리고 이를 모두 포함할 수 있는 것이 바로
원본 이미지의 데이터 분포에서 크게 벗어나지 않는 것입니다.
Diversity는 말 그대로 생성된 이미지가 비슷비슷한 이미지를 만드는 것이 아닌 다양한 이미지를 만들어내고
있냐의 척도입니다. 2개의 평가 척도에 관련된 자세한 정보는 해당 논문을 참조해주세요.
<Density and Recall>
그래서 이 2가지를 평가하기 위해 이 논문에서 주장하는 metric은 Density(for fidelity)와 coverage(for diversity) 입니다.
먼저 이 metric을 적용하기 전에 원본 이미지와 생성된 이미지를 특정한 vector 공간에 embedding을 해야합니다.
이렇게 embedding을 하는 이유는 원 이미지의 차원이 너무 크기 때문이고 원 이미지에는 불필요한 정보가 많기 때문입니다.
그렇기에 이미지의 핵심적인 특징을 잘 추출할 수 있는 feature extractor를 사용하여 차원이 더 낮은 공간에 embedding하게 됩니다.
Embedding을 하는 방법에는 다양한 차원 축소 기법이 있지만, 현재 이미지를 사용하는 방법에는 pretrained 된 CNN 모델을 사용하는것이 보편적입니다. CNN 모델은 이미지의 특징을 정말 잘 추출하기에 보편적으로 사용되지만 모델이 학습한 데이터의 분포와 평가하려는 데이터의 분포가 너무 상이한 경우에는 문제가 생길 수 있다는 점이 한계라고 생각됩니다.
이렇게 embedding된 vector들이 공간상에서 어떤 manifold를 형성하면서 분포하고 있는지 직관적으로 이해하기 위해 해당 논문에서는
k-nearest neighborhood로 manifold를 형성합니다. 즉, 하나의 백터에서 euclidean-distance가 가까운 데이터 k개를 포함할 수 있는 가장 짧은 거리를 해당 데이터의 manifold로 가정합니다. 이러한 방법으로 manifold를 형성한 뒤, 직관적인 방법으로 fidelity와 diversity을 정의합니다.
Density는 원본 이미지로 생성된 manifold 상에 생성된 이미지가 어느 정도의 밀도로 포함되는지에 대한 비율입니다. 즉, 이에 해당하는 비율이 높을수록 생성된 이미지가 manifold내에 밀도높게 분포하고 있다는 뜻이고 원본 데이터 셋의 분포를 벗어나지 않으므로 원본 데이터의 특징을 잘 잡아내어 이미지를 잘 생성한다고 생각할 수 있습니다.
이와 반대로 coverage(=diversity)는 원본 이미지로 생성된 manifold 전체 중에 생성된 이미지가 몇개의 manifold에 속하는지에 대한 비율입니다. 직관적으로 생각해보면 원본 이미지 manifold 내에 좁은 공간에서만 데이터를 생성한다면 fidelity는 높을지언정 diversity가 크다고 할 수 없을 것입니다. 원본 이미지 분포를 전체적으로 포괄하는 분포를 생성해야 diversity가 높다고 볼 수 있습니다. 그런 의미에서 recall은 원본 이미지의 분포를 모두 고려한 비율이므로 diversity를 고려할 수 있습니다. 해당 2개의 metric은 아래의 이미지를 보면 더욱 직관적으로 이해할 수 있습니다.
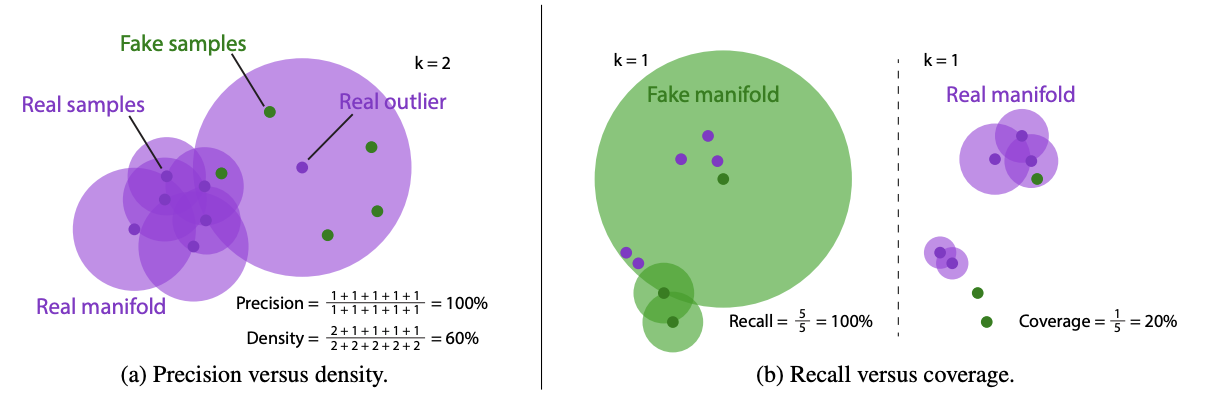


그림에서의 precision과 recall은 이 논문 전에 nvidia에서 발표한 생성모델에 대한 metric으로 해당 논문에서는 이 두개의 metric이 outlier에 너무 민감하게 반응한다는 점을 들어 density와 coverage가 더욱 reliable한 metric임을 주장하고 있습니다. 그리고 이들이 주장하는 metric은 analytic한 유도가 가능하다는 점을 들고 있는데 이와 관련된 유도와 다양한 GAN을 사용해 생성한 이미지들에 대해 실험한 결과는 본 논문을 참조해주세요.
마지막으로 해당 metric은 기존에 생성모델의 평가로 사용되던 FID, IS등의 metric의 fidelity와 diversity를 구별하여 평가할 수 없던 단점을 극복하고 outlier에도 덜 민감한 metric임에는 분명하다고 생각합니다. 하지만 density의 정의상 값이 100%를 넘을 수 있어 절대적인 평가 값으로 사용할 수가 없다는 점, 실제로 생성되는 data의 분포가 k-nearest neighborhood로 이루어진 manifold를 정확하게 따를 것인지에 대한 고민이 필요하다고 생각됩니다.