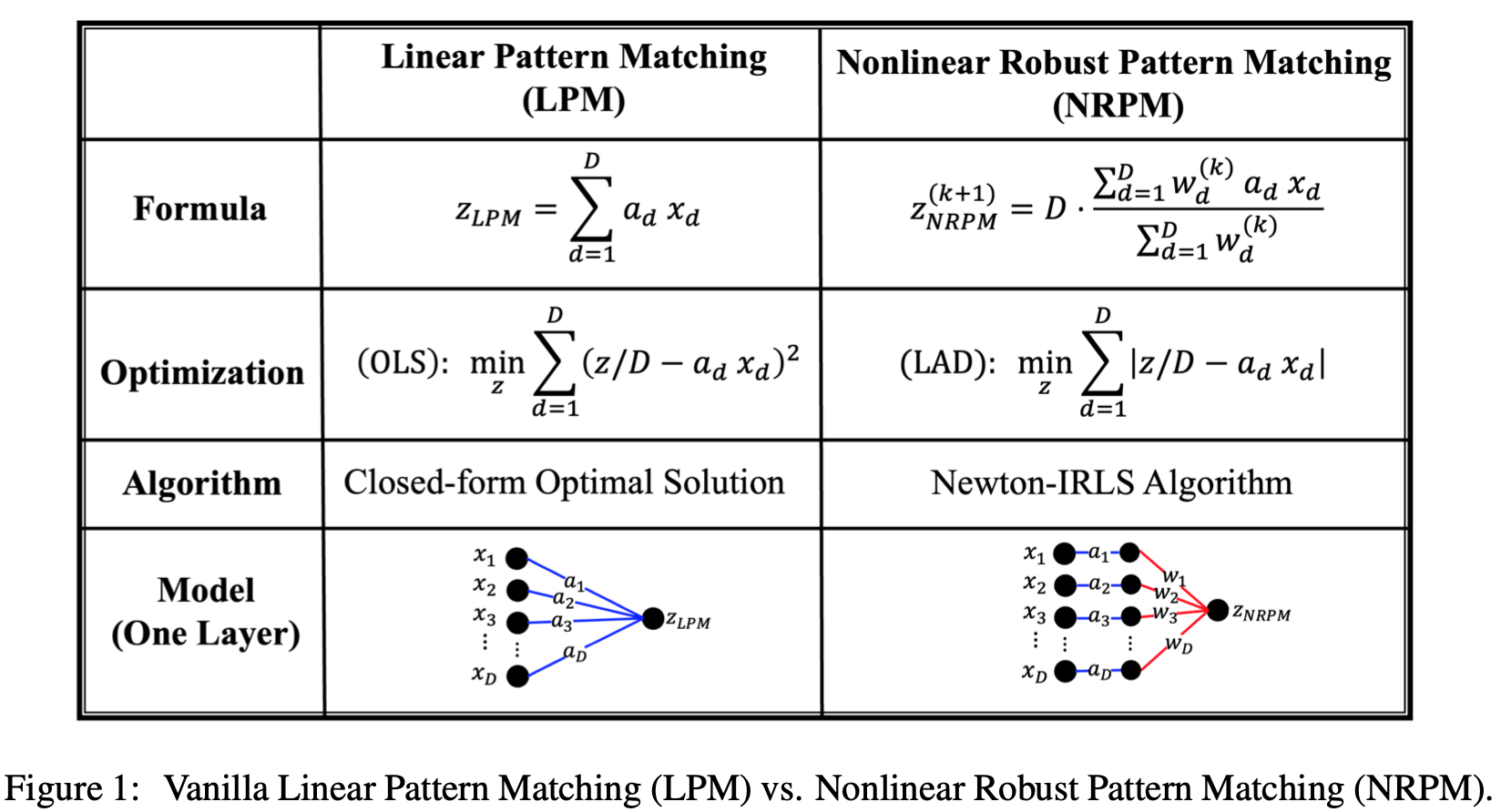
안녕하세요 KDST 한용진입니다.
이번 세미나에서는 2025년도 ICLR에서 발표된 "Robustness Reprogramming for Representation Learning"이란 논문을 발표하였습니다.
논문에 대해 간략하게 먼저 설명을 해보자면, 본 논문에서는 feature의 패턴 매칭 관점에서 신경망 모델의 취약점을 살펴보고 이를 해결하기 위해 비선형 패턴 매칭 방법을 제안합니다. 비선형 패턴 매칭을 통해 유도된 아키텍처로 변환하는 것만으로도 모델의 robustness가 향상됨을 보입니다. Robustness 향상을 위해 고비용의 적대적 학습을 하였던 기존 방법을 벗어나 representation learning 관점으로 재해석하여 추가적인 학습 없이도 robustness를 향상할 수 있음을 보여주는 재밌는 논문입니다.
Introduction
모델의 robustness 향상을 위해 일반적으로 적대적 학습 (adversarial training)과 적대적 정화 (adversarial purification)과 같은 방법을 사용합니다. 그러나 이러한 방법론은 시간 복잡도 및 계산 복잡도가 증가하는 단점이 존재합니다. 본 논문에서는 이러한 단점을 가진 방법을 사용하는 것이 아닌, representation learning의 패턴 매칭 관점에서 추가적인 학습 없이 robustness를 향상시킬 수 있는 방법을 제안합니다.
Notation
feature dimension $D$, input feature $x=(x_1,...,x_D)^T\in \mathcal{R}^D$, parameter vector $a=(a_1,...,a_D)^T\in \mathcal{R}^D$
Nonlinear Robust Pattern Matching
MLP, CNN, Transformer 등의 아키텍처는 다음과 같은 선형 변환을 통해 관심 있는 특정 feature 패턴을 찾기 위한 모델이라고 해석할 수 있습니다: $z=a^Tx=\sum^{D}_{d=1}a_d\cdot x_d$. 특히 어떠한 패턴 $x$가 모델의 파라미터 $a$와 매우 밀접하게 연관되어 있다면, 해당 패턴은 패턴 매칭을 통해 탐지될 수 있습니다. 하지만 이러한 선형 변환은 perturbation에 민감하다는 문제가 있습니다. 이러한 점을 해결하기 위해 Nonlinear Robust Pattern Matching 방법을 제안합니다.
우선, Linear Pattern matching (LPM)을 Ordinary Least Squares (OLS) 문제의 closed-form solution으로 표현할 수 있습니다. 하지만 quadratic penalty로 인해 이상치에 매우 민감하므로 OLS 추정을 Least Absolute Deviation (LAD)에 기반한 식으로 변환합니다.
LAD 식은 non-smooth 하기 때문에 Lemma 3.1을 통해 LAD의 상한을 구하고 이를 newton method로 근사함으로써 미분 가능한 식을 얻습니다: $Z_{LRPM}^{(k+1)}=D\cdot \frac{\sum_{d=1}^Dw_d^{(k)}a_dx_d}{\sum_{d=1}^D w_d^{(k)}}$
Robust Analysis
이러한 비선형 패턴 매칭 방법은 변화율을 통해서 robustness가 향상될 수 있음을 보일 수 있습니다. LPM의 경우 perturbation $x_0$과 $z_{LPM}/D$에 의해 민감도가 결정이 됩니다. NRPM의 경우 NPM과 유사하게 perturbation $x_0$과 $z_{NRPM}/D$에 의해 민감도가 결정되지만, 분모의 $\sum_{d=1}^Dw_d$만큼 민감도 변화가 줄어들기에 좀 더 robust해진다고 주장합니다.
Reprogramming Paradigm
본 논문에서는 NPM과 NRPM을 $\lambda \cdot LPM + (1-\lambda) \cdot LRPM$으로 혼합하여 사용하는 세 가지 패러다임을 제안합니다.
Paradigm 1: fine-tuning 없이 NRPM을 적용
Paradigm 2: $\lambda$만 학습, 추가적인 fine-tuning 없음
Paradigm 3: $\lambda$와 모델 파라미터 모두 fine-tuning
Experiments
NRPM을 적용했을 때 실험 결과는 다음과 같습니다. MNIST, CIFAR10 데이터셋에 대해서 더 높은 robust accuracy를 보였으며 paradigm 3을 통해 모든 파라미터를 fine-tuning 하였을 때 제일 높은 성능을 보여주고 있습니다.
적대적 학습을 함께 적용했을 때에는 더 높은 robustness를 보여주고 있습니다.
Conclusion
본 논문에서는 큰 비용을 들이지 않고도 비선형 패턴 매칭을 통해 robustness를 향상시키는 방법을 제안합니다. 다양한 데이터 셋에서 진행한 실험이 이를 뒷받침해주고 있으며, robust 모델을 만들기 위한 연구에 새로운 방향성을 제시하는 연구입니다. 다만 아쉬운 점은 대부분의 실험이 MNIST에서 이루어졌으며 실험에 사용된 모델 또한 작은 모델이었다는 점이 한계인 것 같습니다.
본 글에서 다루지 않은 증명, 실험들은 아래 논문에서 확인하실 수 있습니다.
