Seeking Consistent Flat Minima for Better Domain Generalization via Refining Loss Landscapes
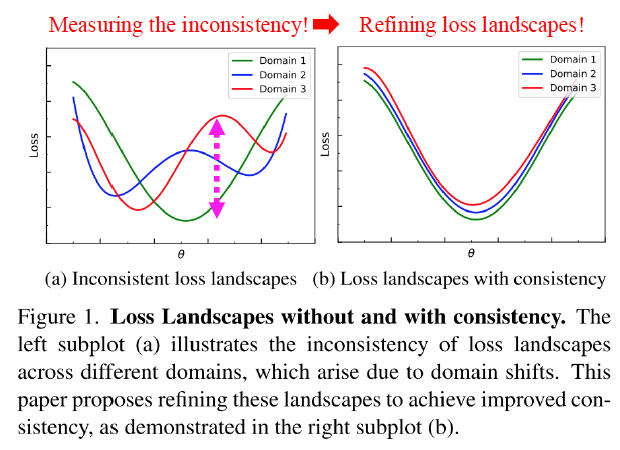
카테고리 없음 2025. 7. 19. 02:16안녕하세요 KDST 한용진입니다.
이번 논문 세미나에서 소개해드린 논문, "Seeking Consistent Flat Minima for Better Domain Generalization via Refining Loss Landscapes"을 살펴보고자 합니다.
논문 제목을 통해 유추할 수 있듯이 loss landscape를 조정해 가며 Domain Generalization을 위해 consistent flat minima를 찾는 방법을 제안하는 논문입니다.
Summary
Domain Generalization을 위해서 여러 연구들이 flat minima를 효율적으로 찾는 방법을 제안해오고 있습니다. 그러나 기존 방법들은 서로 다른 도메인 간의 consistency를 고려하지 않는다는 문제점이 존재합니다. 특히나 loss landscape가 도메인에 따라 다르다면 학습 도메인에서는 flat minima였으나 테스트 도메인에서는 sharp minima일 가능성이 존재합니다. 이러한 문제는 결국 일반화 성능을 저해하는 결과를 야기합니다. 본 논문에서는 이를 해결하기 위해 여러 도메인의 loss landscape를 점진적으로 수정하는 Self-Feedback Training (SFT) 방법을 제안합니다.
Self-Feedback Training framework
SFT는 feedback phase와 refinement phase 두 단계로 이루어져 있습니다. Feedback phase에서는 도메인 간에 inconsistency를 계산하여 이를 feedback signal를 구하는 단계입니다. Refinement phase에서는 feedback signal을 바탕으로 여러 도메인들의 loss landscape를 비슷하게 만들어주는 작업을 진행합니다. 이 과정을 반복하여 Figure 1 (a)에서 Figure 1. (b)와 같은 결과를 얻는 것을 목표로 합니다.
Feedback phase
Feedback phase는 다음과 같이 진행됩니다. 우선 학습 도메인 데이터셋에서 도메인을 무작위로 선택하여 $D_d$와 $D_{d'}$을 구성합니다. 이때 $D_d$는 학습에 활용되고 $D_{d'}$은 도메인 간 inconsistency를 구하는 데 사용됩니다. 모델의 파라미터 $\theta$를 업데이트한 이후에는 feedback signal을 생성합니다. Feedback signal은 맨 처음 구분하였던 $D_d$와 $D_{d'}$간의 sharpness 차이로 정의됩니다.
landscape refiner $g_{\phi}$는 soft label (SL) $y^{(d)}_i$를 출력으로 생성합니다. Feedback phase에서는 one-hot label을 soft label로 대체하여 모델을 학습시킵니다. (위 수식은 모두 y를 y로 바꾼 것이라 보면 됩니다.)
또한 training loss 함수를 landscape refiner $g_{\phi}$의 파라미터에 의존하도록 함으로써 추후에 loss landscape을 변형할 수 있도록 하였습니다. 다만 파라미터 $\phi$는 feedback phase에서는 업데이트되지 않기 때문에 상수로 취급하는 것에 유의해야 합니다.
Feedback signal은 두 도메인 간 sharpness 차이로 정의된다고 언급하였습니다. 물론 loss 값을 사용할 수도 있지만 이는 zero-order info.이기 때문에 그보다는 second-order info.를 반영하는 Hessian과 연관된 sharpness를 사용하는 것이 feedback으로써의 역할을 더 잘 수행할 것이므로 sharpness를 사용하였습니다.
Refinement phase
Refinement phase는 feedback signal을 바탕으로 landscape refiner $g_{\phi}$를 학습하는 과정입니다. 이 과정에서 label의 correctness을 유지하는 것과 soft label이 domain generalization에 도움을 준다는 사실을 중요하게 생각하였습니다. 이에 따라 일반적인 cross-entropy loss를 사용할 수도 있었지만, 그렇게 되면 one-hot target에 overfitting하게 되고 결국 generalization 능력에 제한이 생기는 문제가 발생할 수 있습니다. 대신 저자들은 각 클래스에서의 soft label의 분포 '거리'를 최소화하는 것에 초점을 맞췄습니다. 이는 KL divergence를 통해 달성할 수 있는데 좀 더 효과적인 학습을 위해 Lagrange function과 KKT condition을 사용해 최적화된 soft label 분포를 학습시켰습니다. 본 논문에서는 이를 Projected Cross Entropy (PCE)라고 소개하며 자세한 내용은 논문의 supplementary를 참고하시기 바랍니다.
결국 refinement phase의 최종 loss는 PCE loss, SAM loss, feedback singal로 구성됨을 알 수 있습니다.
전체 알고리즘은 아래와 같습니다.
Experiments
세 개의 클래스와 네 개의 도메인으로 이루어진 데이터셋을 생성하여 실험한 결과입니다. Figure 2에서 첫 번째 행은 SFT를 사용하지 않아 loss landscape가 불규칙적이며 optimal minima또한 미세하게 다른 반면, SFT를 통해 시각화된 도메인의 경우 loss landscape가 일정하며 optimal minima 또한 거의 같은 것을 확인할 수 있습니다.
ResNet50 에 대해서 SAM이 ERM보다 좋으며 SFT가 SOTA 성능을 보여주는 것을 확인할 수 있습니다.
ViT 모델에서의 실험 또한 비슷한 양상을 보이고 있습니다. 신기한 것은 full fine-tuning보다 VPT로 학습한 것이 성능이 더 좋다는 것입니다.
SFT는 SAM variant라고 볼 수도 있는데 다른 SAM variant 방법보다도 더 우수한 성능을 보여주는 것을 확인했습니다.
Sharpness value 또한 오히려 SAM보다 더 낮은 것을 확인할 수 있습니다.
Refinement phase에서 hyper param.으로 사용된 $\lambda$에 대한 ablation study입니다. 상위 파트는 ERM과 SAM을 의미합니다. 물론 SFT가 좋은 성능을 보이지만, SFT에서 소개된 방법들을 추가할 때마다 성능이 향상되는 것을 볼 수 있습니다.
Conclusion
본 논문에서는 도메인 간에 발생할 수 있는 inconsistency를 sharpness를 이용한 feedback signal과 loss landscape refinement를 통해 Domain Generalization 성능을 향상시키는 방법을 제안하였습니다. 비록 테스트 도메인을 알 수 없는 상황이지만 학습 도메인의 loss landscape를 consistent하게 만드는 것만으로도 일반화 성능을 향상시킬 수 있다는 부분이 개인적으로 흥미로웠던 것 같습니다.
잘못 전달한 부분이나 추가적인 질문이 있으시면 댓글 남겨주세요. 감사합니다.
본 글에서 다루지 않은 내용이 있으니 더 깊은 이해를 위해 논문 읽기를 권장드립니다.
