안녕하세요. KDST에서 현장실습을 하고 있는 성균관대학교 데이터사이언스융합전공 김지환이라고 합니다.
제가 오늘 소개드릴 논문은 2020년 NeurIPS에 나온 논문으로, OOD 탐지할 때 사용할 수 있는 score로 Energy score를 제시합니다. 기존에 사용하였던 softmax score의 단점인 overconfidence를 줄일 수 있는 차별화된 방법이라고 저자들은 주장합니다.
NeurIPS 버전과 아카이브 버전이 달라서 두 버전 모두 링크를 달아두겠습니다.
[NeurIPS 버전]
https://proceedings.neurips.cc/paper/2020/file/f5496252609c43eb8a3d147ab9b9c006-Paper.pdf
[아카이브 버전]
https://arxiv.org/pdf/2010.03759.pdf
저자들은 이 논문의 contribution으로 아래와 같은 점들을 주장합니다.
1. Energy score는 기존 OOD score 보다 학습 데이터 x에 대한 확률적 분포를 잘 잡아낼 수 있다.
2. Energy score는 inference 시에 사용하여 OOD를 잘 탐지한다.
3. Energy score로 fine-tuning 시의 loss 함수로도 사용하여 OOD detection을 할 수 있으며, 성능도 준수하다.
1. Preliminary
리뷰에 앞서, 알아야 할 것들이 몇 가지 있습니다.
1. OOD가 무엇인지?
2. Energy가 무엇인지?
1-1. OOD detection
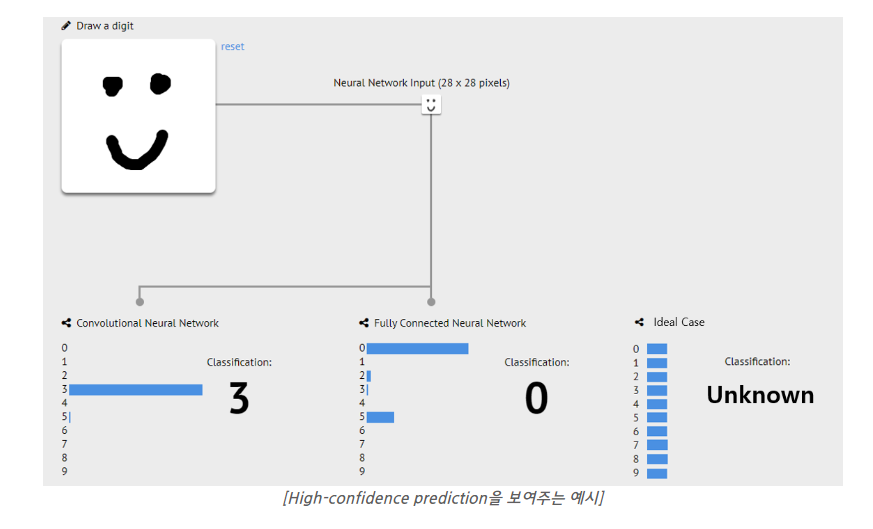
출처: https://hoya012.github.io/blog/anomaly-detection-overview-2/
0부터 9까지의 숫자가 적힌 사진 데이터로 0부터 9까지 분류할 수 있는 모델이 있다고 생각해볼 수 있습니다.
이때 모델에 고양이 사진이 들어간다면, 모델은 어떤 값을 결과값으로 도출해야할까요?
당연히 0부터 9까지 숫자 중 어떤 값으로라도 결과값으로 도출해서는 안될 것입니다.
모델이 0부터 9까지의 확률값으로 결과를 뱉어낸다면, [0.1, 0.1, 0.1, ..., 0.1]로 모두 동일하게 도출해내야 할 것입니다.
위와 같이 모델이 학습했던 0~9 사이의 숫자 사진이 아닌 고양이 사진을 모델이 학습했던 데이터의 분포에 바깥에 있다는 의미에서 Out of Distribution이라고 합니다.
모델의 결과값으로 아무런 결과를 도출해내지 않는 (각 라벨에 동일한 확률값을 뱉어내는) 것을 OOD를 탐지해낸다고 합니다.
1-2. Energy
Statistical learning이나 machine learning의 주요 목적을 "여러 변수들(X,Y)간의 상관관계를 어떻게 하면 잘 인코딩해볼까" 라고 합니다.
이렇게 변수들간의 상관관계(X, Y 간의 상관관계)를 데이터로부터 잘 학습하고 나면, 모르는 변수의 값이 들어왔을 때 이미 알고 있는 변수들의 값을 바탕으로 모델이 질문에 답을 할 수 있을 것입니다.
따라서 학습을 energy의 관점에서 얘기해보면, 데이터를 바탕으로 어떤 energy surface를 만들어 나가되 데이터가 살고 있는 부분 혹은 공간에 대해서는 낮은 energy를 할당하고 다른 부분에는 높은 energy를 할당하도록 하는 그런 과정이라고 생각할 수 있습니다.
즉, 인코딩을 해줄 값 = energy가 되는 것이고 이를 인코딩하는 함수 = energy function이 되는 것입니다.
energy function이 학습되는 과정, 즉 energy surface가 만들어지는 과정은 아래와 같이 생각해볼 수 있습니다.

여기서 학습한 데이터와 가까울 때 에너지가 낮은 이유는, 에너지가 낮을수록 안정적이라는 물리적 개념을 차용하기 위함이라고 합니다.
현재 우리가 하고자 하는 OOD detection task를 떠올려보면, 우리는 ID와 OOD를 구분하는 energy surface를 만들어주는 energy function을 학습하고자 하는 것으로 이해할 수 있습니다.
이때 에너지 값은 스칼라 값으로, 우리는 이 값을 이용해서 특정 threshold보다 작으면 ID로, 이보다 크면 OOD로 판별할 것입니다.
이해를 돕기 위해 위 논문에서 발췌한 그림을 첨부하겠습니다.

1-3. Energy function
이 논문에서 사용하는 Energy function은 흔히 사용하는 logit에 temperature scaling을 한 버전입니다.
저자들은 이전에 나온 ODIN이라는 논문에서 제안한 temperature scaling이 OOD detection에 효과적이었다는 아이디어를 착안하여, temperature scaling을 제안한다. 이때 temperature T는 1보다 큰 값으로 해서 1/T를 logit에 곱해 softmax를 취합니다.

위의 식은 K개의 클래스, 즉 K차원의 logit vector의 output에 T의 역수를 곱하고, 이를 Negative Log Likelihood를 계산합니다.
그리고 energy based model의 pdf는 아래와 같습니다. (T가 1인 상황에서)

그리고 이를 우리가 사용하고자 하는 pdf로 변환하면 아래와 같이 표현할 수 있습니다.

이때 분모의 경우는 전체 데이터 x에 대한 energy를 더하는 항(partition function)인데, 이를 우리가 구할 수 없습니다. 따라서 로그 연산을 취해 분모의 영향을 지워버립니다.

위 식이 중요한 이유는 softmax와는 달리, x의 확률적 분포와 일치하게 energy 함수를 사용할 수 있다는 것에 있습니다. 또한, 두번째 term이 모든 x에 대해 상수값이므로 ID에 대해 낮은 에너지를 부여할 수 있고, OOD에 대해 높은 에너지를 부여할 수 있습니다.
그리고 분류기를 하나 두어서, 에너지가 특정 threshold를 넘으면 OOD로 그렇지 않으면 ID로 판별할 수 있도록 구성합니다.

2. Energy Score vs. Softmax Score
이전에 OOD를 탐지할 때는 softmax를 취해 가장 높은 값을 score로 두고, 이 값을 threshold와 비교하여 OOD를 판별했습니다.
하지만 저자들은 이 방법에 문제가 있다고 합니다.
아래에 우리가 알고 있는 softmax값 중 가장 큰 값을 뽑아내는 softmax confidence score로부터 enegy score를 유도해보도록 하겠습니다. (이때 energy score의 T는 1이라고 가정합니다.)

앞선 공식에서,

를 이용해 softmax confidence를 다시 한번 써보면 아래와 같이 쓸 수 있습니다.
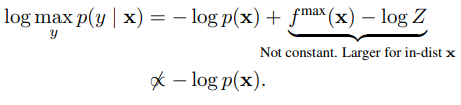
우리의 OOD score는 ID에 대해 낮고, OOD에 대해 높길 원하는데, 위의 식에서 뒤의 두 항은 ID에 대해 높은 값을 부여할 수 있습니다.
때문에 Energy score에 비해 bias가 생길 수밖에 없다.
3. Energy-bounded Learning for OOD Detection
저자들은 fine-tuning 시에 OOD를 탐지할 수 있도록 기존 cross entropy loss 함수에 새로운 term을 제시합니다.
fine-tuning할 때는 ID 데이터와 보조 OOD data가 쌍으로 동시에 들어가는 상황입니다.

이 규제항은 아래와 같습니다.

이 항은 hinge loss로, ID data가 m_in이라는 ID data에 대한 energy threshold(m_in)보다 크면 loss를 부여하고, 반대로 OOD data가 OOD data에 대한 energy threshold(m_out)보다 작으면 loss를 부여하는 방식입니다.
4. Experiment
실험 결과를 보기 전, FPR95라는 metric을 소개하고자 합니다.
이 논문에서 FPR95는 ID 샘플에 대해 true positive 비율이 95%일 때, OOD 샘플의 false positive 비율을 뜻합니다.
저자들은 CIFAR10으로 사전학습한 WideResNet에 대해 SVHN 데이터셋으로 inference할 때의 OOD Metric인 FPR95와 softmax score(a)와 energy score(b), 그리고 사전학습한 WideResNet에 대해 CIFAR10과 SVHN 쌍으로 inference 할 때의 FPR95와 softmax score(c)와 energy score(d)를 보여주는 figure를 제시했습니다.

확실히 softmax score의 overconfidence를 줄여주는 것을 (a)와 (b)를 통해 알 수 있습니다.
그리고 다양한 데이터셋으로 실험하였을 때의 FPR95 performance를 제시하였습니다.
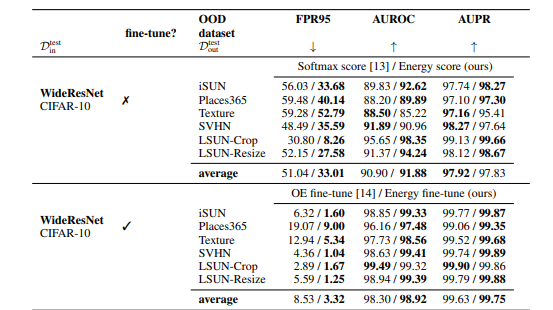
fine-tuning한 것과 inference 결과를 같이 report 해둔 figure도 함께 첨부합니다.

이렇게 Energy-based Out-of-distribution Detection 논문에 대한 리뷰를 마쳐보도록 하겠습니다.
읽어주셔서 감사합니다.