KDST

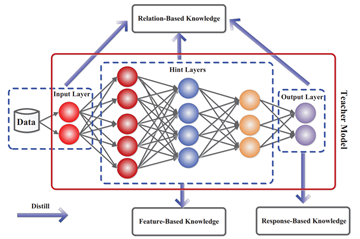
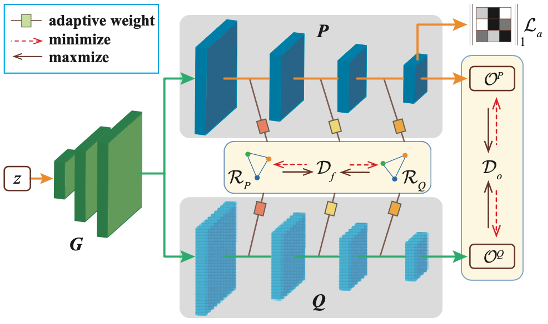
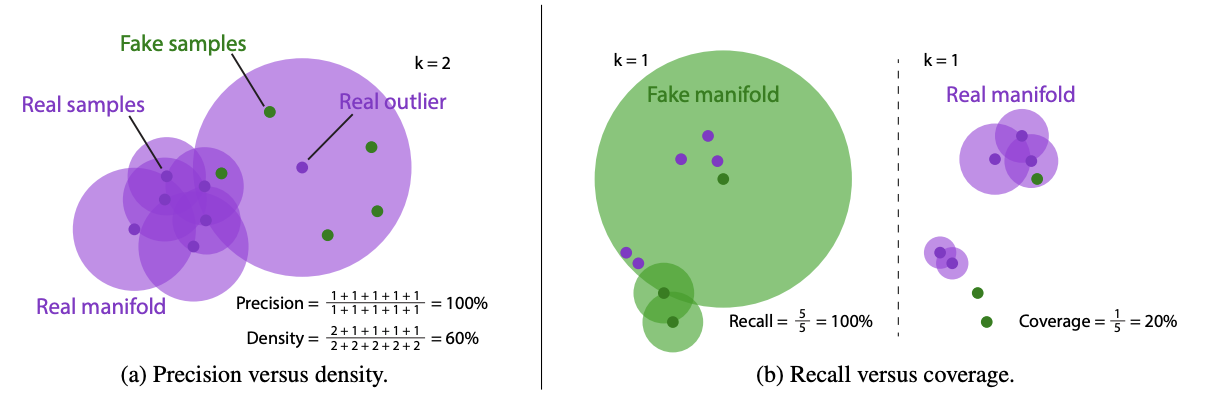
이번에는 CVPR 2020에 Oral session에 발표된 논문인 Revisiting Knowledge Distillation via Label Smoothing Regularization을 리뷰하려고 합니다. 논문은 링크를 참조해주세요 Background Geoffrey Hinton 이 2014년 NeurIPS에 발표한 Distilling the Knowledge in a Neural Network 이후로 분야가 개척되어왔습니다. Knowledge Distillation에서 Hinton이 발표한 방식은 pretrained teacher model의 logits과 student모델의 logits의 soft-target을 구해서 KL Divergence를 취해서 서로 분포간의 거리를 좁히는 방식으로 학습..

이번에는 NIPS 2020 Poster session에 발표된 논문인 AdaShare: Learning What To Share For Efficient Deep Multi-Task Learning 을 리뷰하려고 합니다. 논문은 링크를 참조해주세요 Background and Introduction 우선 Mutli-task learning이라는 게 어떤 것일까요? Multi-task learning은 task가 여러 개라는 것인데 큰 dataset $D$ 아래에 다른 dataset $D_{i}$로 구분된 $D=\{D_1, ... , D_i \}$ 를 사용하는 learning method를 말합니다. Multi-task learning의 종류에는 크게 두 가지 기준인 feature와 method으로 분류합니..

이번 글에서는 CVPR 2021에 oral로 선정된 “Knowledge Evolution in Neural Networks”란 논문을 소개합니다. 본 논문은 적은 수의 데이터 셋에서 모델을 효과적으로 학습시킬 수 있는 Knowledge evolution이라는 학습 방법론을 제안합니다. History 본 논문은 “The lottery ticket hypothesis: Finding sparse, trainable neural networks” 논문을 이론 배경으로 가집니다. The Lottery ticket hypothesis는 dense network에 적은 iteration 수에서 자신보다 높은 성능을 가지지만 파라미터 수는 더 적은 subnetwork가 존재한다 라는 것입니다. 이러한 가설에 맞는 s..

이번 글에서는 NeurIPS에 Spotlight로 선정된 “Temporal Spike Sequence Learning via Backpropagation for Deep Spiking Neural Networks” 논문을 소개해드리려고 합니다. 해당 논문의 자세한 내용은 링크와 github를 참고해주세요 Introduction - Spiking Neural Network(SNN)은 뇌의 행동을 모방하여 동작할 수 있는 모델로 기존 DNN(Deep Neural Network)와 달리 Time data 또한 영향을 끼치는 모델입니다. 최근 DNN의 많은 에너지 사용 대신 효율적으로 사용하는 뇌를 모방하여 전성비를 올리기 위한 목적으로 Neuronmorphic chip과 더불어 SNN이 개발되고 있습니다. -..

이번 글에서는 NIPS 2020에 oral로 선정된 “Compositional Explanations of Neurons”란 논문을 소개합니다. 해당 논문은 XAI의 interpretability 연구 중 하나로 제안하는 방식을 통해 explanation을 생성하고 이를 통해 Vision과 NLP 딥러닝 모델에 대한 분석을 진행합니다. History 기존의 Neural network interpretability 연구들은 사람에게 친숙한 explanation을 생성하기 위해 모델 시각화 정보나 입력 수동 검사를 해야하는 한계가 있었습니다. 따라서 최근 “probing datasets”을 사용하여 데이터의 레이블을 이용한 자동 설명 생성 방식이 등장하였습니다. 하지만 이러한 방식은 뉴런의 기능을 atomi..

오늘 소개드릴 논문은 "Zero-shot Adversarial Quantization"으로 CVPR 2021에 oral paper로 accept된 논문입니다. 해당 논문을 참조하시려면 논문링크와 github을 참고해주세요 관련논문 DFQ: Data-Free Quantization Through Weight Equalization and Bias Correction ACIQ: Analytical Clipping For Integer Qunatization of Neural Networks ZeroQ: A Novel Zero shot Quantization Framework GDFQ : Generative Low-bitwidth Data Free Quantization Overview 양자화 논문이지만 새로..

Generative model(생성 모델) 기존의 데이터셋 X의 분포를 근사하는 새로운 data를 생성하는 것으로 기존의 데이터셋 x이 나타날 수 있는 확률 분포 p(x)를 구하는 것이라고 생각할 수 있습니다. 이는 기존의 discriminative model과는 차이점이 있는데, discriminative model이란 데이터 x가 주어졌을때, 그에 해당하는 레이블 Y가 나타날 수 있는 조건부 확률 P(x|y)를 구하는 것 입니다. 그렇기 때문에 discriminative model은 레이블 y정보가 있어야 하기 때문에 supervised learning의 범주에 속합니다. 이와 반대로 generative model은 레이블 y에 대한 정보없이 데이터 x를 주고 P(x|x) = P(x)로 근사하는 확률..

본 게시글은 Generative Adversarial Networks(GAN)를 공부하며 흥미로웠던 CycleGAN에 대한 포스팅입니다. 해당 논문은 버클리 AI Research (BAIR) lab에서 진행된 연구로, 2017년 ICCV에 accept되었습니다. 해당 논문을 참조하시려면 논문 링크를 클릭해주세요. CycleGAN은 training set이 {X,Y} 처럼 paired data가 아닌 unpaired된 data인 경우, source 도메인 X에서 target 도메인 Y로 이미지를 변환하는 image-to-image translation 방식입니다. 아래의 예시는 CycleGAN을 활용했을때의 두가지의 도메인에 대해서 이미지를 translation 하는 예시입니다. 이러한 두가지 도메인에 대..

저희 팀이 참여하는 "고위험 재난의료 및 산업재해 대응기술 개발" 과제가 선정되었습니다. 과제 내에서 저희 팀의 역할은 센서로부터의 생체 신호를 딥러닝 기술 등에 기반한 시계열 분석으로 중증도 예측 등으로 활용하는 내용은 맡게 되었습니다. 재미있는 주제이고 과제 규모도 적지 않은 만큼 열심히 수행해서 좋은 결과 내도록 최선을 다할 생각입니다.

안녕하세요, KDST에서 인턴 연구원으로 근무했던 김우정입니다. 이번에 김수현 박사님, 박민철 인턴 연구원님, 전근석 학연님과 함께 제출했던 논문이 NeurIPS (NIPS) 2020에 poster presentation으로 accept 되었습니다. 논문 제목은 "Neuron Merging: Compensating for Pruned Neurons" 입니다. 기존 structured network pruning 논문들에서는 신경망에서 덜 중요한 뉴런이나 필터를 제거하고 accuracy를 회복하기 위하여 fine-tuning을 합니다. 하지만 이때 제거된 뉴런에 상응하는 다음 layer의 차원 또한 제거됩니다. 따라서 pruning 직후에 다음 layer의 output feature map이 원래 모델과 ..