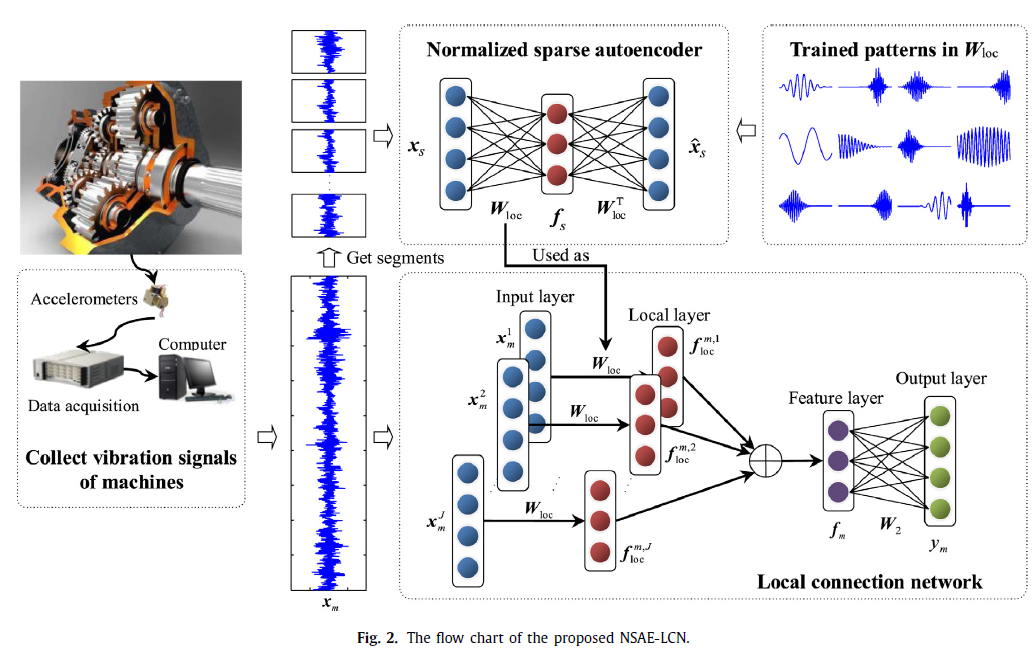
본 게시물은 필자가 2019년 12월 8일부터 진행되었던 NeurIPS 논문중에서 인상깊었던 논문 및 아이디어를 포스팅 한 것입니다. 본 포스팅은 논문에 첨부된 그림을 첨부했으며 문제가 될 시 삭제하도록 하겠습니다. 또한 본 포스팅은 Deep Q Network에 대한 기본 지식을 가지고 있다는 전제하에 작상된 포스팅입니다. Deep Q-Network에 대한 내용은 아래의 링크를 참조하시길 바랍니다. 논문 링크는 이곳을 클릭해주세요. Sample-Efficient Deep Reinforcement Learning via Episodic Backward Update 강화학습을 실제 환경에 적용하기에는 쉽지 않습니다. Aracade Learning 환경에서 Deep Q-Network를 사용하여 학습을 시킬 시..